Euler's number e
The number e is an important mathematical constant that is the base of the natural logarithm. It is approximately equal to 2.71828,[and is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series[2]
The constant can be defined in many ways; for example, e is the unique real number such that the value of the derivative (slope of the tangent line) of the function f(x) = ex at the point x = 0 is equal to 1.[3] The function ex so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base e. The natural logarithm of a positive number k can also be defined directly as the area under the curve y = 1/x between x = 1 and x = k, in which case, e is the number whose natural logarithm is 1. There are also more alternative characterizations.
Alternative characterizations
See also: Representations of e
Other characterizations of e are also possible: one is as the limit of a sequence, another is as the sum of an infinite series, and still others rely on integral calculus. So far, the following two (equivalent) properties have been introduced:1. The number e is the unique positive real number such that
3. The number e is the limit
5. The number e is the unique positive real number such that


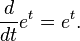


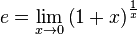
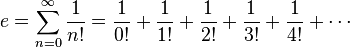

No comments:
Post a Comment