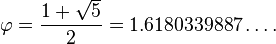Charles Emile Pickard (1856-1941) French Mathematics Professor

Along with Simeon-Denis Picard was the most important and distinguished French mathematician of the day.

Piccard's Method
Pickard's method, sometimes called the method of successive approximations, gives a means of proving the existence of solutions to differential equations.

Émile Picard
Born	(1856-07-24)24 July 1856 Paris, France
Died	11 December 1941(1941-12-11) (aged 85) Paris, France
Nationality	French
Fields	Mathematics
Institutions	University of Paris
Alma mater	École Normale Supérieure
Doctoral advisor	Gaston Darboux
Doctoral students	Sergei Bernstein Lucien Blondel Gheorghe Calugareanu Paul Dubreil Jacques Hadamard Gaston Julia Traian Lalescu Philippe Le Corbeiller Paul Painlevé Mihailo Petrović Simion Stoilow Ernest Vessiot Henri Villat André Weil Stanisław Zaremba
Known for	Picard functor Picard group Picard theorem Picard variety Picard–Lefschetz formula Picard–Lindelöf theorem Painlevé transcendents
Notable awards	Fellow of the Royal Society[1]

Picard's mathematical papers, textbooks, and many popular writings exhibit an extraordinary range of interests, as well as an impressive mastery of the mathematics of his time. Modern students of complex variables are probably familiar with two of his named theorems. His lesser theorem states that every nonconstant entire function takes every value in the complex plane, with perhaps one exception. His greater theorem states that an analytic function with an essential singularity takes every value infinitely often, with perhaps one exception, in any neighborhood of the singularity. He made important contributions in the theory of differential equations, including work on Picard–Vessiot theory, Painlevé transcendents and his introduction of a kind of symmetry group for a linear differential equation. He also introduced the Picard group in the theory of algebraic surfaces, which describes the classes of algebraic curves on the surface modulo linear equivalence. In connection with his work on function theory, he was one of the first mathematicians to use the emerging ideas of algebraic topology.
..

PI Sherif Monem

PI =  3 +  0.14  15   92  65

PI = 3 + 1/7

PI =  3 + 1/( 7 + (1/16) )

PI =  3 + 1/(7  + (1000/15997))  =  3 + 0.14 15  92  68

PI                                                =  3 + 0.14 15  92  65  Tables

PI  = 3 + 1/(7  + (1001/16012))  =  3 + 0.14 15  92  60

PI  = 3 + 1/(7  + (1001/16013))  =  3 + 0.14 15  92  68
 

The Golden Rule Triangle

Line segments in the golden ratio

A golden rectangle (in pink) with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship .

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,

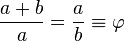where the Greek letter phi ( or ) represents the golden ratio. Its value is:

 A001622

The golden ratio also is called the golden mean or golden section (Latin: sectio aurea).^[1][2][3] Other names include extreme and mean ratio,^[4] medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut,^[5] and golden number.^[6][7][8]
Some twentieth-century artists and architects, including Le Corbusier and Dalí, have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be
//

Euler's number e Video

 

 

Vocal Tract Picture Illustration

The number e mathematical constant is the base of the natural logarithm.

Euler's number e

The number e is an important mathematical constant that is the base of the natural logarithm. It is approximately equal to 2.71828,^[and is the limit of (1 + 1/n)ⁿ as n approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series^[2]

The constant can be defined in many ways; for example, e is the unique real number such that the value of the derivative (slope of the tangent line) of the function f(x) = e^x at the point x = 0 is equal to 1.^[3] The function e^x so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base e. The natural logarithm of a positive number k can also be defined directly as the area under the curve y = 1/x between x = 1 and x = k, in which case, e is the number whose natural logarithm is 1. There are also more alternative characterizations.

Alternative characterizations

The area between the x-axis and the graph y = 1/x, between x = 1 and x = e is 1.

See also: Representations of e

Other characterizations of e are also possible: one is as the limit of a sequence, another is as the sum of an infinite series, and still others rely on integral calculus. So far, the following two (equivalent) properties have been introduced:
1. The number e is the unique positive real number such that

2. The number e is the unique positive real number such that

The following three characterizations can be proven equivalent:
3. The number e is the limit

Similarly:

4. The number e is the sum of the infinite series

where n! is the factorial of n.

5. The number e is the unique positive real number such that

research in graph theory prove that all maps could be colored using only four colors

Much research in graph theory was motivated by attempts to prove that all maps, like this one, could be colored using only four colors so that no areas of the same color touched. Kenneth Appel and Wolfgang Haken proved this in 1976.^[5]