The Golden Rule Triangle

Line segments in the golden ratio

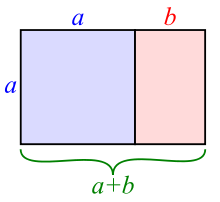
A golden rectangle (in pink) with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship .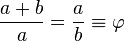

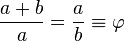In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,

where the Greek letter phi ( or ) represents the golden ratio. Its value is:

 A001622

The golden ratio also is called the golden mean or golden section (Latin: sectio aurea).^[1][2][3] Other names include extreme and mean ratio,^[4] medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut,^[5] and golden number.^[6][7][8]
Some twentieth-century artists and architects, including Le Corbusier and Dalí, have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be
//